Computer Organization and Structure

Homework #4

Due: 2011/12/20

1. We wish to add the instructions jr (jump register), sll (shift left logical), lui (load upper immediate), and a variant of the lw (load word) instruction to the single-cycle datapath. The variant of the lw instruction increments the index register after loading word from memory. This instruction (l_inc) corresponds to the following two instructions:

lw $rs, L($rt)

addi $rt, $rt, 1

Add any necessary datapaths and control signals to Figure 1 and show the necessary additions to Table 1. You can photocopy Figure 1 and Table 1 to make it faster to show the additions.

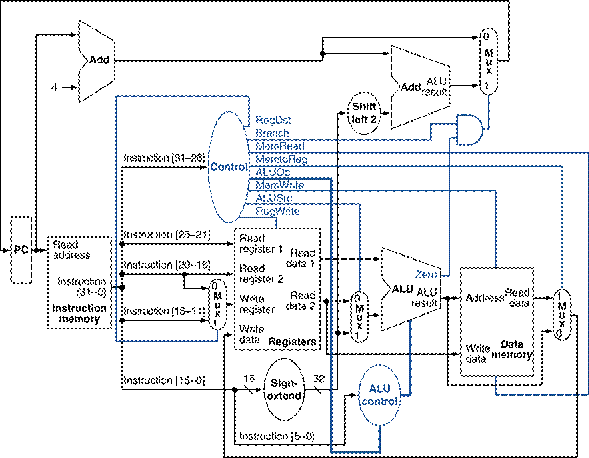
Figure 1: The simple datapath with the control unit.

Instruction	RegDst	ALUSrc	Memto Reg	Reg Write	Mem Read	Mem Write	Branch	ALUOp1	ALUOp0
R-format	1	0	0	1	0	0	0	1	0
lw	0	1	1	1	1	0	0	0	0
sw	X	1	X	0	0	1	0	0	0
beq	X	0	X	0	0	0	1	0	1

Table 1: The setting of the control lines is completely determined by the opcode fields of the instruction.

2. Assuming the following latencies for logic blocks in the datapath:

	I-Mem	Add	Mux	ALU	Regs	D-Mem	Sign-extend	Shift-left-2
a.	400ps	100ps	30ps	120ps	200ps	350ps	20ps	0ps
b.	500ps	150ps	100ps	180ps	220ps	1000ps	90ps	20ps

a. What is the clock cycle time if the only type of instructions we need to support are ALU instructions (add, and, etc.)?

b. What is the clock cycle type if we only had to support lw instructions?

c. What is the clock cycle time if we must support add, beq, lw, and sw instructions?

For the remaining problems, assume that there are no pipeline stalls and that the breakdown of executed instructions is as follows:

	add	addi	not	beq	lw	sw
a.	30%	15%	5%	20%	20%	10%
b.	25%	5%	5%	15%	35%	15%

a. In what fraction of all cycles is the data memory used?

b. In what fraction of all cycles is the input of the sign-extend circuit needed? What is this circuit doing in cycles in which its input is not needed?

c. If we can improve the latency of one of the given datapath components by 10%, which component should it be? What is the speed-up from this improvement?

3. The following problems refer to the following fragment of MIPS code:

	Instruction sequence
a.	lw $1, 40($6) beq $2, $0, Label ; Assume $2 = $0 sw $6, 50($2) Label: add $2, $3, $4 sw $3, 50($4)
b.	lw $5, -16($5) sw $4, -16($4) lw $3, -20($4) beq $2, $0, Label ; Assume $2 != $0 add $5, $1, $4

a. For this problem, assume that all branches are perfectly predicted (this eliminates all control hazards) and that no delay slots are used. If we only have one memory (for both instructions and data), there is a structural hazard every time we need to fetch an instruction in the same cycle in which another instruction accesses data. To guarantee forward progress, this hazard must always be resolved in favor of the instruction that accesses data. What is the total execution of this instruction sequence in the five-stage pipeline that only has one memory? We have seen that data hazards can be eliminated by adding nops to the code. Can you do the same with this structural hazard? Why?

b. For this problem, assume that all branches are perfectly predicted (this eliminates all control hazards) and that no delay slots are used. If we change load/store instructions to use a register (without an offset) as the address, these instructions no longer need to use the ALU. As a result, MEM and EX stages can be overlapped and the pipeline has only four stages. Change this code to accommodate this changed ISA. Assuming this change does not affect clock cycle time, what speed-up is achieved this instruction sequence?

c. Assuming stall-on-branch and no delay slots, what speed-up is achieved on this code if branch outcomes are determined in the ID stage, relative to the execution where branch outcomes are determined in the EX stage?

The remaining problems assume that individual pipeline stages have the following latencies:

	IF	ID	EX	MEM	WB
a.	100ps	120ps	90ps	130ps	60ps
b.	180ps	100ps	170ps	220ps	60ps

d. Given these pipeline stage latencies, repeat the speed-up calculation from subquestion b., but take into account the (possible) change in clock cycle time. When EX and MEM are done in a single stage, most of their work can be done in parallel. As a result, the resulting EX/MEM stage has a latency that is the larger of the original two, plus 20ps needed for the work that could not be done in parallel.

e. Given these pipeline stage latencies, repeat the speed-up calculation from subquestion c., taking into account the (possible) change in clock cycle time. Assume that the latency ID stage increases by 50% and the latency of the EX stage decreases by 10ps when branch outcome resolution is moved from EX to ID.

f. Assuming stall-on-branch and no delay slots, what is the new clock cycle time and execution time of this instruction sequence if beq address computation is moved to the MEM stage? What is the speed-up from this change? Assume that the latency of the EX stage is reduced by 20ps and the latency of the MEM stage is unchanged when branch outcome resolution is moved from EX to MEM.

4. Assuming the following repeating pattern (e.g., in a loop) of branch outcomes:

	Branch outcomes
a.	T, T, NT, T
b.	T, T, T, NT, NT

a. What is the accuracy of always-taken and always-out-taken predictors for this sequence of branch outcomes?

b. What is the accuracy of the two-bit predictor for the first four branches in this pattern, assuming that the predictor starts off in the bottom left state from Figure 2 (predict not taken).

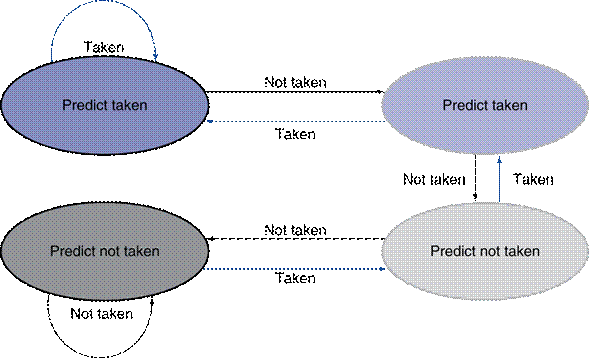
Figure 2: The states in a 2-bit prediction scheme.

c. What is the accuracy of the two-bit predictor if this pattern is repeated forever?

d. Design a predictor that would achieve a perfect accuracy if this pattern is repeated forever. Your predictor should be a sequential circuit with one output that provides a prediction (1 for taken, 0 for not taken) and no inputs other than the clock and the control signal that indicates that the instruction is a conditional branch.

e. What is the accuracy of your predictor from the above subquestion if it is given a repeating pattern that is the exact opposite of this one?