Computer Organization and Structure

Homework #3

Due: 2006/11/14

1. Convert 4096_ten, -2,047_ten, and -2,000,000_ten into 32-bit two’s complement binary numbers, respectively, and convert the following two’s complement binary numbers to be decimal numbers:

a. 1111 1111 1111 1111 1111 1111 0000 0110_two;

b. 1111 1111 1111 1111 1111 1111 1110 1111_two;

c. 0111 1111 1111 1111 1111 1111 1110 1111_two.

2. The following MIPS instruction sequence could be used to implement a new instruction that has two register operands. Give the instruction a name and describe what it does. Note that register $t0 is being used as a temporary.

srl $s1, $s1, 1 #

sll $t0, $s0, 31 # These 4 instructions accomplish “new $s0 $s1”

srl $s0, $s0, 1 #

or $s1, $s1, $t0 #

3. The ALU supported set on less than (slt) using just the sign bit of the adder. Let’s try a set on less than operation using the values -7_ten and 6_ten. To make it simpler to follow the example, let’s limit the binary representations to 4 bits: 1001_two and 0110_two.

1001_two – 0110_two = 1001_two + 1010_two = 0011_two

This result would suggest that -7_ten > 6_ten, which is clearly wrong. Hence we must factor in overflow in the decision. Modify the 1-bit ALU in the following figures to handle slt correctly.

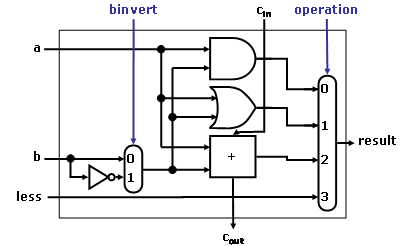
Figure 1: A 1-bit ALU that performs AND, OR, and addition on a and b or b’.

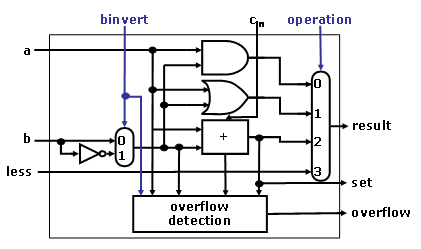
Figure 2: A 1-bit ALU for the most significant bit.

4. Add 2.85_ten x 10³ to 9.84_ten x 10⁴ and add 3.63_ten x 10⁴ to 6.87_ten x 10³, respectively, assuming that you have only three significant digits, first with guard and round digits and then without them.

5. Given the bit pattern:

1010 1101 0001 0000 0000 0000 0000 0010

what does it represent, assuming that it is

a. a two’s complement integer?

b. an unsigned integer?

c. a single precision floating-point number?

d. a MIPS instruction?